8.2. Ignorance pdfs: Indifference and translation groups

Original version by Christian Forssén (Department of Physics, Chalmers University of Technology, Sweden) and Daniel Phillips (Department of Physics and Astronomy, Ohio University), Oct 23, 2019.

Minor updates by Dick Furnstahl, November, 2021.

Discrete permutation invariance

• Consider a six-sided die

• How do we assign \(p_i \equiv p(X_i|I)\), \(i \in \{1, 2, 3, 4, 5, 6\}\)?

• We do know \(\sum_i p(X_i|I) = 1\)

• Invariance under labeling \(\Rightarrow p(X_i|I)=1/6\)

  • provided that the prior information \(I\) says nothing that breaks the permutation symmetry.

Location invariance

Indifference to a constant shift \(x_0\) for a location parameter \(x\) implies that

\[ p(x|I) dx \approx p(x+ x_0|I) d(x+x_0) = p(x+ x_0|I) dx, \]

in the allowed range.

Location invariance implies that

\[ p(x|I) = p(x+ x_0|I) \quad \Rightarrow \quad p(x|I) = \mathrm{constant}. \]

• Provided that the prior information \(I\) says nothing that breaks the symmetry.

• The pdf will be zero outside the allowed range (specified by \(I\)).

Scale invariance

Indifference to a re-scaling \(\lambda\) of a scale parameter \(x\) implies that

\[ p(x|I) dx \approx p(\lambda x|I) d(\lambda x) = \lambda p(\lambda x|I) dx, \]

in the allowed range.

Invariance under re-scaling implies that

\[ p(x|I) = \lambda p(\lambda x|I) \quad \Rightarrow \quad p(x|I) \propto 1/x. \]

• Provided that the prior information \(I\) says nothing that breaks the symmetry.

• The pdf will be zero outside the allowed range (specified by \(I\)).

• This prior is often called a Jeffrey’s prior; it represents a complete ignorance of a scale parameter within an allowed range.

• It is equivalent to a uniform pdf for the logarithm: \(p(\log(x)|I) = \mathrm{constant}\)

  • as can be verified with a change of variable \(y=\log(x)\), see lecture notes on error propagation.

Example: Straight-line model

Consider the theoretical model

\[ y_\mathrm{th}(x) = \theta_1 x + \theta_0. \]

• Would you consider the intercept \(\theta_0\) a location or a scale parameter, or something else?

• Would you consider the slope \(\theta_1\) a location or a scale parameter, or something else?

Consider also the statistical model for the observed data \(y_i = y_\mathrm{th}(x_i) + \epsilon_i\), where we assume independent, Gaussian noise \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\).

• Would you consider the standard deviation \(\sigma\) a location or a scale parameter, or something else?

Symmetry invariance

• In fact, by symmetry indifference we could as well have written the linear model as \(x_\mathrm{th}(y) = \theta_1' y + \theta_0'\)

• We would then equate the probability elements for the two models

\[ p(\theta_0, \theta_1 | I) d\theta_0 d\theta_1 = q(\theta_0', \theta_1' | I) d\theta_0' d\theta_1'. \]

• The transformation gives \((\theta_0', \theta_1') = (-\theta_1^{-1}\theta_0, \theta_1^{-1})\).

This change of variables implies that

\[ q(\theta_0', \theta_1' | I) = p(\theta_0, \theta_1 | I) \left| \frac{d\theta_0 d\theta_1}{d\theta_0' d\theta_1'} \right|, \]

where the (absolute value of the) determinant of the Jacobian is

\[\begin{split} \left| \frac{d\theta_0 d\theta_1}{d\theta_0' d\theta_1'} \right| = \mathrm{abs} \left( \begin{vmatrix} \frac{\partial \theta_0}{\partial \theta_0'} & \frac{\partial \theta_0}{\partial \theta_1'} \\ \frac{\partial \theta_1}{\partial \theta_0'} & \frac{\partial \theta_1}{\partial \theta_1'} \end{vmatrix} \right) = \frac{1}{\left( \theta_1' \right)^3}. \end{split}\]

• In summary we find that \(\theta_1^3 p(\theta_0, \theta_1 | I) = p(-\theta_1^{-1}\theta_0, \theta_1^{-1}|I).\)

• This functional equation is satisfied by

\[ p(\theta_0, \theta_1 | I) \propto \frac{1}{\left( 1 + \theta_1^2 \right)^{3/2}}. \]

100 samples of straight lines with fixed intercept equal to 0 and slopes sampled from three different pdfs. Note in particular the prior preference for large slopes that results from using a uniform pdf.

The principle of maximum entropy

Having dealt with ignorance, let us move on to more enlightened situations.

Consider a die with the usual six faces that was rolled a very large number of times. Suppose that we were only told that the average number of dots was 2.5. What (discrete) pdf would we assign? I.e. what are the probabilities \(\{ p_i \}\) that the face on top had \(i\) dots after a single throw?

The available information can be summarized as follows

\[ \sum_{i=1}^6 p_i = 1, \qquad \sum_{i=1}^6 i p_i = 2.5 \]

This is obviously not a normal die, with uniform probability \(p_i=1/6\), since the average result would then be 3.5. But there are many candidate pdfs that would reproduce the given information. Which one should we prefer?

It turns out that there are several different arguments that all point in a direction that is very familiar to people with a physics background. Namely that we should prefer the probability distribution that maximizes an entropy measure, while fulfilling the given constraints.

It will be shown below that the preferred pdf \(\{ p_i \}\) is the one that maximizes

\[ Q\left( \{ p_i \} ; \lambda_0, \lambda_1 \right) = -\sum_{i=1}^6 p_i \log(p_i) + \lambda_0 \left( 1 - \sum_{i=1}^6 p_i \right) + \lambda_1 \left( 2.5 - \sum_{i=1}^6 i p_i \right), \]

where the constraints are included via the method of Lagrange multipliers.

The entropy of Scandinavians

Let’s consider another pdf assignment problem. This is originally the kangaroo problem (Gull and Skilling, 1984), but translated here into a Scandinavian context. The problem is stated as follows:

Information: :
70% of all Scandinavians have blonde hair, and 10% of all Scandinavians are left handed.

Question: :
On the basis of this information alone, what proportion of Scandinavians are both blonde and left handed?

We note that for any one given Scandinavian there are four distinct possibilities:

1. Blonde and left handed (probability \(p_1\)).

2. Blonde and right handed (probability \(p_2\)).

3. Not blonde and left handed (probability \(p_3\)).

4. Not blonde and right handed (probability \(p_4\)).

The following 2x2 contingency table

	left handed	right handed
blonde	\(p_1\)	\(p_2\)
not blonde	\(p_3\)	\(p_4\)

can be written in terms of a single variable \(x\) due to the normalization condition \(\sum_{i=1}^4 p_i = 1\), and the available information \(p_1 + p_2 = 0.7\) and \(p_1 + p_3 = 0.1\)

	left handed	right handed
blonde	\(0\le x\le 0.1\)	\(0.7-x\)
not blonde	\(0.1-x\)	\(0.2+x\)

But which choice of \(x\) is preferred?

The monkey argument

The monkey argument is a model for assigning probabilities to \(M\) different alternatives that satisfy some constraint as described by \(I\):

• Monkeys throwing \(N\) balls into \(M\) equally sized boxes.

• The normalization condition \(N = \sum_{i=1}^M n_i\).

• The fraction of balls in each box gives a possible assignment for the corresponding probability \(p_i = n_i / N\).

• The distribution of balls \(\{ n_i \}\) divided by \(N\) is therefore a candidate pdf \(\{ p_i \}\).

After one round the monkeys have distributed their (large number of) balls over the \(M\) boxes.

• The resulting pdf might not be consistent with the constraints of \(I\), however, in which case it should be rejected as a possible candidate.

• After many such rounds, some distributions will be found to come up more often than others. The one that appears most frequently (and satisfies \(I\)) would be a sensible choice for \(p(\{p_i\}|I)\).

• Since our ideal monkeys have no agenda of their own to influence the distribution, this most favored distribution can be regarded as the one that best represents our given state of knowledge.

Now, let us see how this preferred solution corresponds to the pdf with the largest entropy. Remember in the following that \(N\) (and \(n_i\)) are considered to be very large numbers (\(N/M \gg 1\))

• The logarithm of the number of micro-states, \(W\), as a function of \(\{n_i\}\) follows from the multinomial distribution (where we use the Stirling approximation \(\log(n!) \approx n\log(n) - n\) for large numbers, and there is a cancellation of two terms)

\[ \log(W(\{n_i\})) = \log(N!) − \sum_{i=1}^M \log(n_i!) \approx N\log(N) - \sum_{i=1}^M n_i\log(n_i), \]

• There are \(M^N\) different ways to distribute the balls.

• The micro-states \(\{ n_i\}\) are connected to the pdf \(\{ p_i \}\) and the frequency of a given pdf is given by

\[ F(\{p_i\}) = \frac{\text{number of ways of obtaining } \{n_i\}}{M^N} \]

• Therefore, the logarithm of this frequency is

\[ \log(F(\{p_i\})) \approx -N \log(M) + N\log(N) - \sum_{i=1}^M n_i\log(n_i) \]

Substituting \(p_i = n_i/N\), and using the normalization condition finally gives

\[ \log(F(\{p_i\})) \approx -N \log(M) - N \sum_{i=1}^M p_i\log(p_i) \]

We note that \(N\) and \(M\) are constants so that the preferred pdf is given by the \(\{ p_i \}\) that maximizes

\[ S = - \sum_{i=1}^M p_i\log(p_i). \]

You might recognise this quantity as the entropy from statistical mechanics. The interpretation of entropy in statistical mechanics is the measure of uncertainty that remains about a system after its observable macroscopic properties, such as temperature, pressure and volume, have been taken into account. For a given set of macroscopic variables, the entropy measures the degree to which the probability of the system is spread out over different possible microstates. Specifically, entropy is a logarithmic measure of the number of micro-states with significant probability of being occupied \(S = -k_B \sum_i p_i \log(p_i)\), where \(k_B\) is the Boltzmann constant.

Why maximize the entropy?

• Information theory: maximum entropy=minimum information (Shannon, 1948).

• Logical consistency (Shore & Johnson, 1960).

• Uncorrelated assignments related monotonically to \(S\) (Skilling, 1988).

Consider the third argument. Let us check it empirically for the problem of hair color and handedness of Scandinavians. We are interested in determining \(p_1 \equiv p(L,B|I) \equiv x\), the probability that a Scandinavian is both left-handed and blonde. However, in this simple example we can immediately realize that the assignment \(p_1=0.07\) is the only one that implies no correlation between left-handedness and hair color. Any joint probability smaller than 0.07 implies that left-handed people are less likely to be blonde, and any larger value indicates that left-handed people are more likely to be blonde.

So unless you have specific information about the existence of such a correlation, you should not build it into the assignment of the probability \(p_1\).

Question: Can you show why \(p_1 < 0.07\) and \(p_1 > 0.07\) corresponds to left-handedness and blondeness being dependent variables?

Hint: The joint probability of left-handed and blonde is \(x\). Using the other expressions in the table, what is this joint probability if the probabilities of being left-handed and of being blonde are independent?

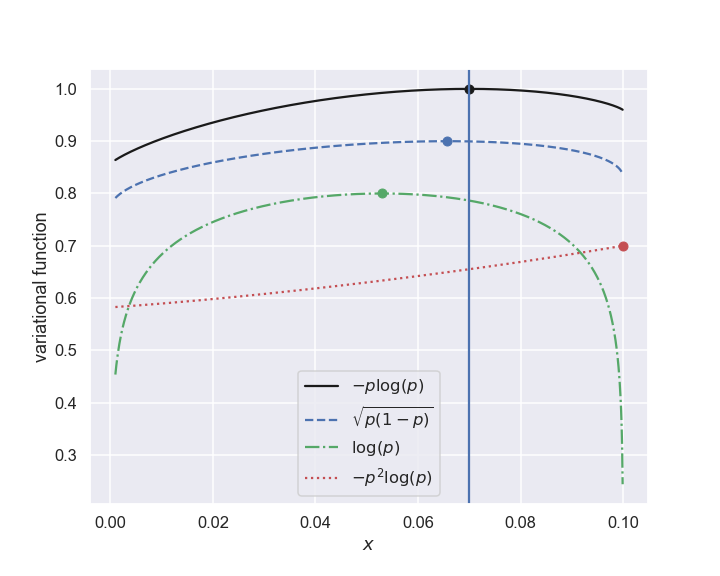
Let us now empirically consider a few variational functions of \(\{ p_i \}\) and see if any of them gives a maximum that corresponds to the uncorrelated assignment \(x=0.07\), which implies \(p_1 = 0.07, \, p_2 = 0.63, \, p_3 = 0.03, \, p_4 = 0.27\). A few variational functions and their prediction for \(x\) are shown in the following table.

Variational function	Optimal \(x\)	Implied correlation
\(-\sum_i p_i \log(p_i)\)	0.070	None
\(\sum_i \log(p_i)\)	0.053	Negative
\(-\sum_i p_i^2 \log(p_i)\)	0.100	Positive
\(-\sum_i \sqrt{p_i(1-p_i)}\)	0.066	Negative

The assignment based on the entropy measure is the only one that respects this lack of correlations.

Four different variational functions \(f\bigl(\{ p_i \}\bigr)\). The optimal \(x\) for each one is shown by a circle. The uncorrelated assignment \(x=0.07\) is shown by a vertical line.

Continuous case

Return to monkeys, but now with different probabilities for each bin. Then

\[ S= −\sum_{i=1}^M p_i \log \left( \frac{p_i}{m_i} \right), \]

which is often known as the Shannon-Jaynes entropy, or the Kullback number, or the cross entropy (with opposite sign).

Jaynes (1963) has pointed out that this generalization of the entropy, including a Leqesgue measure \(m_i\), is necessary when we consider the limit of continuous parameters.

\[ S[p]= −\int p(x) \log \left( \frac{p(x)}{m(x)} \right). \]

• In particular, \(m(x)\) ensures that the entropy expression is invariant under a change of variables \(x \to y=f(x)\).

• Typically, the transformation-group (invariance) arguments are appropriate for assigning \(m(x) = \mathrm{constant}\).

• However, there are situations where other assignments for \(m\) represent the most ignorance. For example, in counting experiments one might assign \(m(N) = M^N / N!\) for the number of observed events \(N\) and a very large number of intervals \(M\).

Derivation of common pdfs using MaxEnt

The principle of maximum entropy (MaxEnt) allows incorporation of further information, e.g. constraints on the mean, variance, etc, into the assignment of probability distributions.

In summary, the MaxEnt approach aims to maximize the Shannon-Jaynes entropy and generates smooth functions.

Mean and the Exponential pdf

Suppose that we have a pdf \(p(x|I)\) that is normalized over some interval \([ x_\mathrm{min}, x_\mathrm{max}]\). Assume that we have information about its mean value, i.e.,

\[ \langle x \rangle = \int dx\, x p(x|I) = \mu. \]

Based only on this information, what functional form should we assign for the pdf that we will now denote \(p(x|\mu)\)?

Let us use the principle of MaxEnt and maximize the entropy under the normalization and mean constraints. We will use Lagrange multipliers, and we will perform the optimization as a limiting case of a discrete problem; explicitly, we will maximize

\[ Q = -\sum_i p_i \log \left( \frac{p_i}{m_i} \right) + \lambda_0 \left( 1 - \sum_i p_i \right) + \lambda_1 \left( \mu - \sum_i x_i p_i \right). \]

Setting \(\partial Q / \partial p_j = 0\) we obtain

\[ p_j = m_j \exp \left[ -(1+\lambda_0) \right] \exp \left[ -\lambda_1 x_j \right]. \]

With a uniform measure \(m_j = \mathrm{constant}\) we find (in the continuous limit) that

\[ p(x|\mu) = \mathcal{N} \exp \left[ -\lambda_1 x \right]. \]

The normalization constant (related to \(\lambda_0\)) and the remaining Lagrange multiplier, \(\lambda_1\), can easily determined by fulfilling the two constraints.

Assuming, e.g., that the normalization interval is \(x \in [0, \infty[\) we obtain

\[ \int_0^\infty p(x|\mu) dx = 1 = \left[ -\frac{\mathcal{N}}{\lambda_1} e^{-\lambda_1 x} \right]_0^\infty = \frac{\mathcal{N}}{\lambda_1} \quad \Rightarrow \quad \mathcal{N} = \lambda_1. \]

The constraint for the mean then gives

\[ \mu = \lambda_1 \int_0^\infty x e^{-\lambda_1 x} dx = \lambda_1 \frac{1!}{\lambda_1^2} = \frac{1}{\lambda_1} \quad \Rightarrow \quad \lambda_1 = \frac{1}{\mu}. \]

So that the properly normalized pdf from MaxEnt principles becomes the exponential distribution

\[ p(x|\mu) = \frac{1}{\mu} \exp \left[ -\frac{x}{\mu} \right]. \]

Variance and the Gaussian pdf

Suppose that we have information not only on the mean \(\mu\) but also on the variance

\[ \left\langle (x-\mu)^2 \right\rangle = \int (x-\mu)^2 p(x|I) dx = \sigma^2. \]

The principle of MaxEnt will then result in the continuum assignment

\[ p(x|\mu,\sigma) \propto \exp \left[ - \lambda_1 ( x - \mu )^2 \right]. \]

Assuming that the limits of integration are \(\pm \infty\) this results in the standard Gaussian pdf

\[ p(x|\mu,\sigma) = \frac{1}{\sigma \sqrt{2\pi}} \exp \left[ - \frac{( x - \mu )^2}{2\sigma^2} \right]. \]

This indicates that the normal distribution is the most honest representation of our state of knowledge when we only have information about the mean and the variance.

Notice.

These arguments extend easily to the case of several parameters. For example, considering \(\{x_k\}\) as the data \(\{ D_k\}\) with error bars \(\{sigma_k\}\) and \(\{\mu_k\}\) as the model predictions, this allows us to identify the least-squares likelihood as the pdf which best represents our state of knowledge given only the value of the expected squared-deviation between our predictions and the data

\[ p\left( \{x_k\} | \{\mu_k, \sigma_k\} \right) = \prod_{k=1}^N \frac{1}{\sigma_k \sqrt{2\pi}} \exp \left[ - \frac{( x_k - \mu_k )^2}{2\sigma_k^2} \right]. \]

If we had convincing information about the covariance \(\left\langle \left( x_i - \mu_i \right) \left( x_j - \mu_j \right) \right\rangle\), where \(i \neq j\), then MaxEnt would assign a correlated, multivariate Gaussian pdf for \(p\left( \{ x_k \} | I \right)\).

Counting statistics and the Poisson distribution

The derivation, and underlying arguments, for the binomial distribution and the Poisson statistic based on MaxEnt is found in Sivia, Secs 5.3.3 and 5.3.4.